Bose-Einstein condensate (BEC) is an extreme state of matter that may occur when bosonic neutral atoms are cooled to very low temperatures (~100 nK). When a BEC is trapped in a magnetic potential, the spin of each atom is oriented in the direction of the magnetic field. The spin degrees of freedom are frozen and the BEC is described by a scalar order parameter. When the BEC is trapped using an optical potential, the spin of each atom is free to evolve. The order parameter of describing a spin-f BEC has 2f+1 component and the BEC is referred to as a spinor BEC. This research project focuses on using spinor BEC for generating metrological useful entangled states.

Recent results

Deterministic entanglement generation from driving through quantum phase transitions^[1]

For a ⁸⁷Rb BEC of zero magnetization in the F=1 ground hyperfine manifold, the spinor ground state of the system exhibits three quantum phases, namely the Polar (P), Broken-axis symmetry (BA), and Twin-Fock (TF) phases. The polar phase is equivalent to a pure BEC with only one m_F=0 component. This phase can be prepared readily in experiment. By tuning the relative strength between the (m_F=0 to m_F=±1) spin-mixing rate (c₂) and the quadratic Zeeman energy (q) of the BEC, we can efficiently drive a polar BEC across two quantum critical points, resulting in a highly entangled TF BEC, a quantum state that allows phase measurement precision beyond the standard quantum limit. The experiment highlights the potential of generating entanglement by driving a system through quantum phase transitions.

[1].  Luo, X. Y., Zou, Y. Q., Wu, L. N., Liu, Q., Han, M. F., Tey, M. K., and You, L., Science 355, 620-623 (2017).

Beating the classical precision limit with spin-1 Dicke states of more than 10,000 atoms^[2]

Dicke states form an important class of highly entangled states which are common eigenstates |l,m〉 of the collective spin operators L² and L_z. Here L≡(L_x,L_y,L_z), L_k = Σ_j=1^N s_k^(j) with s_k^(j) representing the spin operator of the jth particle along the k(=x,y,z) direction. Most Dicke states produced so far are limited to pseudospin-1/2 (two-level) particles. In this work, we deterministically generate balanced spin-1 Dicke states in the close vicinity of |l=N,m=0〉 with N~11700, by driving a spin-1 condensate through a quantum phase transition. The prepared states are characterized to exhibit a collective spin length of l>0.99N and their entanglement breadth is inferred to be more than 10000 on average and at least ~630 atoms at 1 standard deviation. Compared to our previously reported twin-Fock state (spin-1/2 Dicke state), this spin-1 Dicke state takes advantage of all three spin components and offers higher interferometric sensitivity. Using the prepared states, we demonstrate enhanced measurement precision beyond the three-mode standard quantum limit (SQL).

Figure (A) shows the Bloch sphere representation (left) of the three-mode Dicke state. Figure (B) shows the enhancement of measured angular sensitivity over the three-mode SQL using the prepared states.

[2].  Yi-Quan Zou, Ling-Na Wu, Qi Liu, Xin-Yu Luo, Shuai-Feng Guo, Jia-Hao Cao, Meng Khoon Tey, and Li You, Proceedings of the National Academy of Sciences (2018): 201715105.

Nonlinear interferometry beyond classical limit facilitated by cyclic dynamics^[3]

Time-reversed evolution has substantial implications in physics, including prominent applications in refocusing of classical waves or spins and fundamental researches such as quantum information scrambling. In quantum metrology, nonlinear interferometry based on time reversal protocols supports entanglement-enhanced measurements without requiring low-noise detection. Despite the broad interest in time reversal, it remains challenging to reverse the quantum dynamics of an interacting many-body system as is typically realized by an (effective) sign-flip of the system’s Hamiltonian. Here, we present an approach that is broadly applicable to cyclic systems for implementing nonlinear interferometry without invoking time reversal. Inspired by the observation that the time-reversed dynamics drives a system back to its starting point, we propose to accomplish the same by slaving the system to travel along a ‘closed-loop’ instead of explicitly tracing back its antecedent path. Utilizing the quasi-periodic spin mixing dynamics in a three-mode 87Rb atom spinor condensate, we implement such a ‘closed-loop’ nonlinear interferometer and achieve a metrological gain of 3.87 decibels over the classical limit for a total of 26500 atoms. Our approach unlocks the high potential of nonlinear interferometry by allowing the dynamics to penetrate into deep nonlinear regime, which gives rise to highly entangled non-Gaussian state. The idea of bypassing time reversal may open up new opportunities in the experimental investigation of researches that are typically studied by using time reversal protocols.

Three-mode nonlinear interferometry based on by cyclic dynamics. (a) Nonlinear interferometry is typically realized by a pair of time-reversed operations: ‘path’ splitting U1 and recombining U2, with phase encoding Up (orange triangle) sandwiched in between. For a system with cyclic dynamics, the required time reversal can be circumvented by properly timing the instant to complete a periodic return. (b) Schematic illustration for our three-mode nonlinear interferometer based on spin mixing dynamics (SMD) that creates (annihilates) paired atoms. (c) SMD is initiated by a sudden change of quadratic Zeeman shift (QZS) from q>>2|c2| to q=|c2|. (d) Temporal evolution of ρ0 starting with all atoms in the |1, 0> component. The upper panel denotes the ideal case without atom loss or technical noises, where q is set to be 0.99|c2|, while the middle and lower panels present experimentally measured data respectively for fixed q = 0.99|c2| and tuned q(t) = 0.99|c2|e−0.4.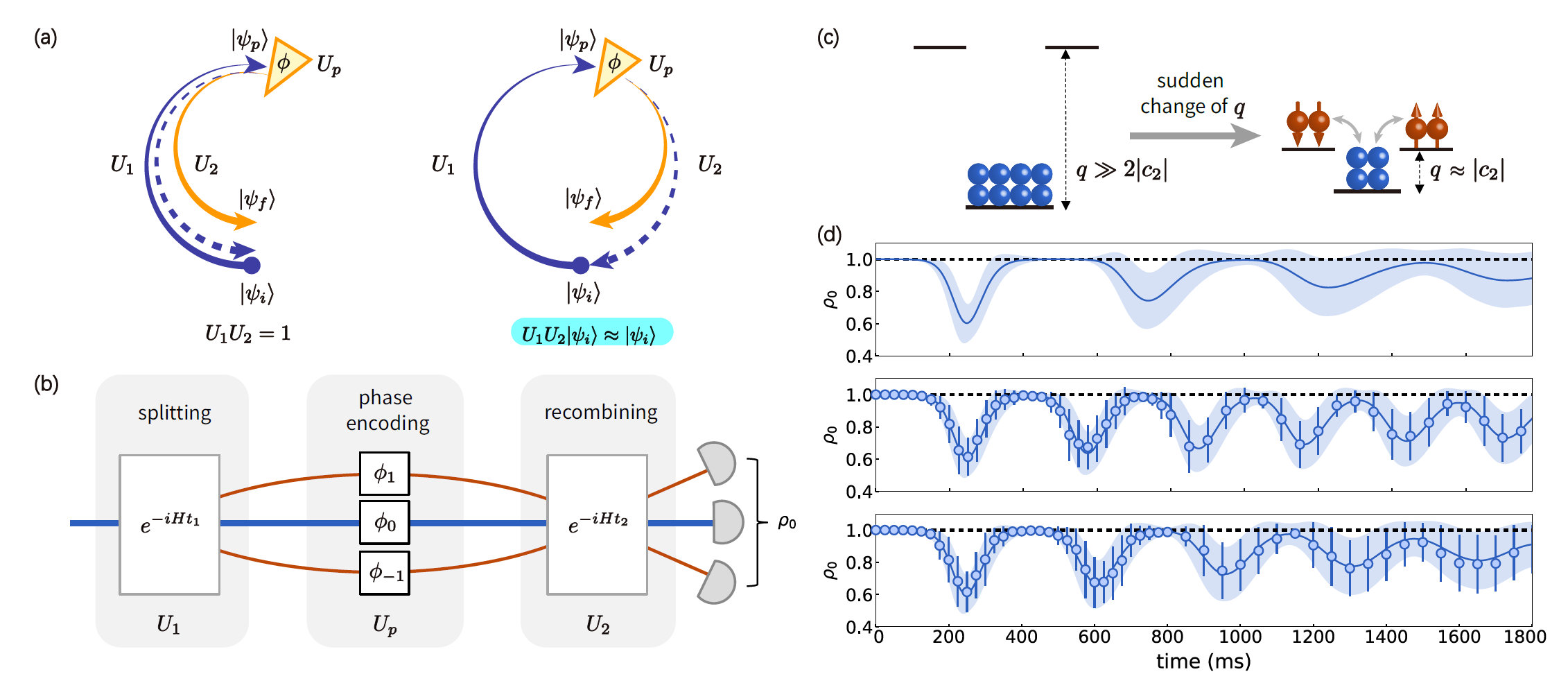

[3]. Qi Liu, Ling-Na Wu, Jia-Hao Cao, Tian-Wei Mao, Xin-Wei Li, Shuai-Feng Guo, Meng Khoon Tey, and Li You, Nature Physics, 18, 167–171(2022).
News & Views "Measure in circles" by Philipp Kunkel & Monika Schleier-Smith, Nature Physics, 124–125 (2022). DOI · PDF

Detection of Entangled States Supported by Reinforcement Learning^[4]

Discrimination of entangled states is an important element of quantum-enhanced metrology. This typically requires low-noise detection technology. Such a challenge can be circumvented by introducing nonlinear readout process. Traditionally, this is realized by reversing the very dynamics that generates the entangled state, which requires a full control over the system evolution. In this Letter, we present nonlinear readout of highly entangled states by employing reinforcement learning to manipulate the spin-mixing dynamics in a spin-1 atomic condensate. The reinforcement learning found results in driving the system toward an unstable fixed point, whereby the (to be sensed) phase perturbation is amplified by the subsequent spin-mixing dynamics. Working with a condensate of 10900 87Rb atoms, we achieve a metrological gain of 6.97dB beyond the classical precision limit. Our work will open up new possibilities in unlocking the full potential of entanglement caused quantum enhancement in experiments.

The principle of RL is shown in the following figure: (A) Illustration of the interaction loop between neural network and simulated system for RL training. (B) Nonlinear interferometry with two RL-designed beam splitters, respectively assuming the roles of “splitting” and “recombining”. The training results for N = 50 particles are shown in (C)-(D): (C) Evolution of fidelity F and fractional population ρ0 during the splitting operation U1 aims at achieving the target probe state (spin-1 Dicke state). (D) Evolution of metrological gain and ρ0 during the recombining operation U2 targets the maximal metrological gain. The blue (orange) solid line denotes results with (without) noise.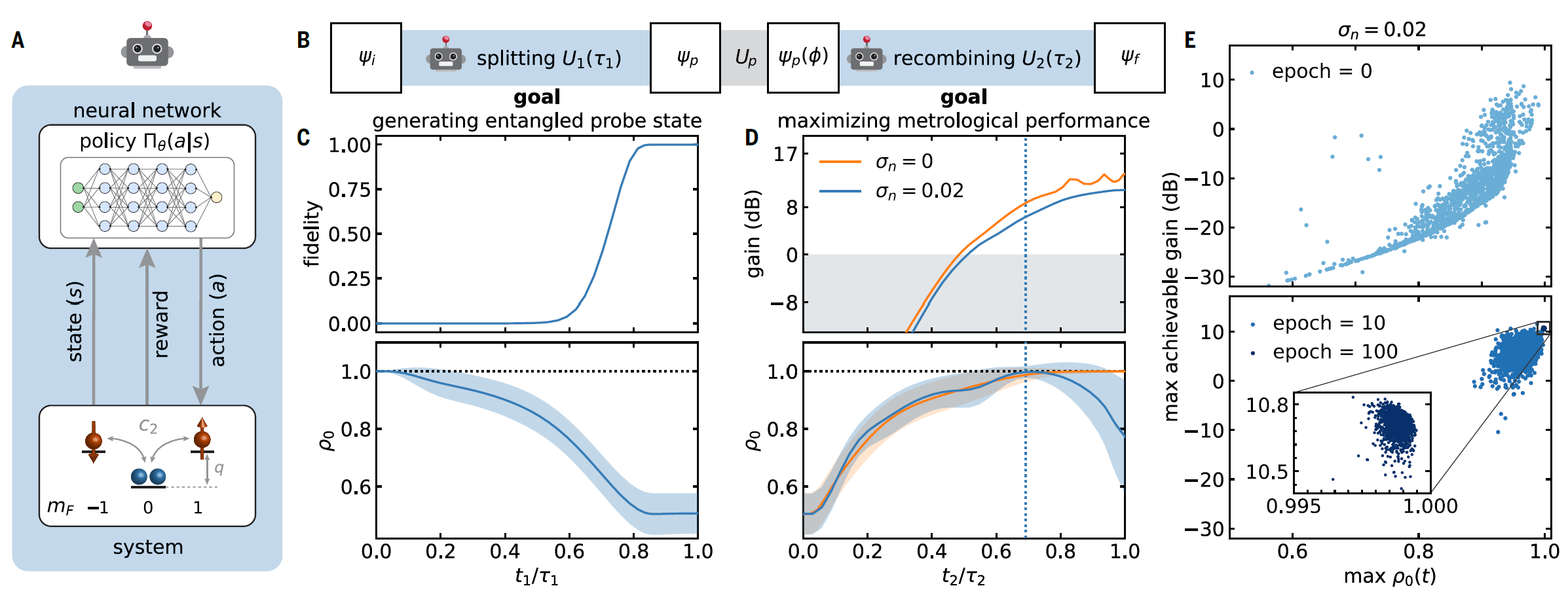

[4].  Jia-Hao Cao, Feng Chen , Qi Liu, Tian-Wei Mao, Wen-Xin Xu, Ling-Na Wu, and Li You, Physical Review Letters (2023): 131, 073201.

Observing 16.5 dB of enhanced phase sensing over classical limit with spin-nematic squeezed atoms^[5]

Quantum entanglement is a proven resource for enhanced measurement precision beyond standard quantum limit (SQL), the highest precision achievable with uncorrelated particles1. Despite substantial efforts, observed enhancements are limited by the abilities to prepare, maintain, and manipulate entanglement, and by detection noise from imperfect counting of particles. Here, we report observing record high phase sensitivity enhancements using nonlinear interferometries with spin-1 atomic Bose-Einstein condensates. Coherent spin-mixing dynamics in a decoherence-free subspace gives rise to highly squeezed entangled state for sensing a single rotation, which is preferentially amplified over measurement noise with subsequent unbalanced effectively time-reversed evolution. The nonlinear interferometry protocol achieves a sensitivity 15.6 ± 0.5 decibels (dB) beyond the two-mode SQL of 26400 atoms for a small-angle rotation induced by radio-frequency magnetic field, which outperforms the 11.7±0.3 dB gain from directly measuring the squeezed probe state, thanks to the enhanced robustness to detection noise with interaction-based readout. Applied to sensing the quadrature phase encoded by a power stabilized microwave field in a full Ramsey interferometry protocol, a metrological gain of 16.5 ± 2.4 dB is achieved, which represents the highest enhancement factor for phase measurement ever reported in any physical system todate. With feasible implementations, our nonlinear interferometers can be applied to diverse precision measurement scenarios such as atomic magnetometer, atomic clock, and momentum entangled interferometry for testing Einstein’s equivalence principle.

The following figure shows nonlinear Rabi interferometry for sensing Lx-rotation. a, Schematic of the interferometry protocol with splitting and recombining. The sequence inside the green dashed-line rectangular box details the nested operations of the state rotation, making it a Rabi interferometer for sensing Lx-rotation. The blue shaded state distribution on the spin-nematic sphere corresponds to the state after Rabi rotation around Lx by an angle ϑ denoted by the short red line segment, which is magnified and shown elongated in the end. In all panels, solid lines are simulation results and dashed lines are fitted curves to experimental data.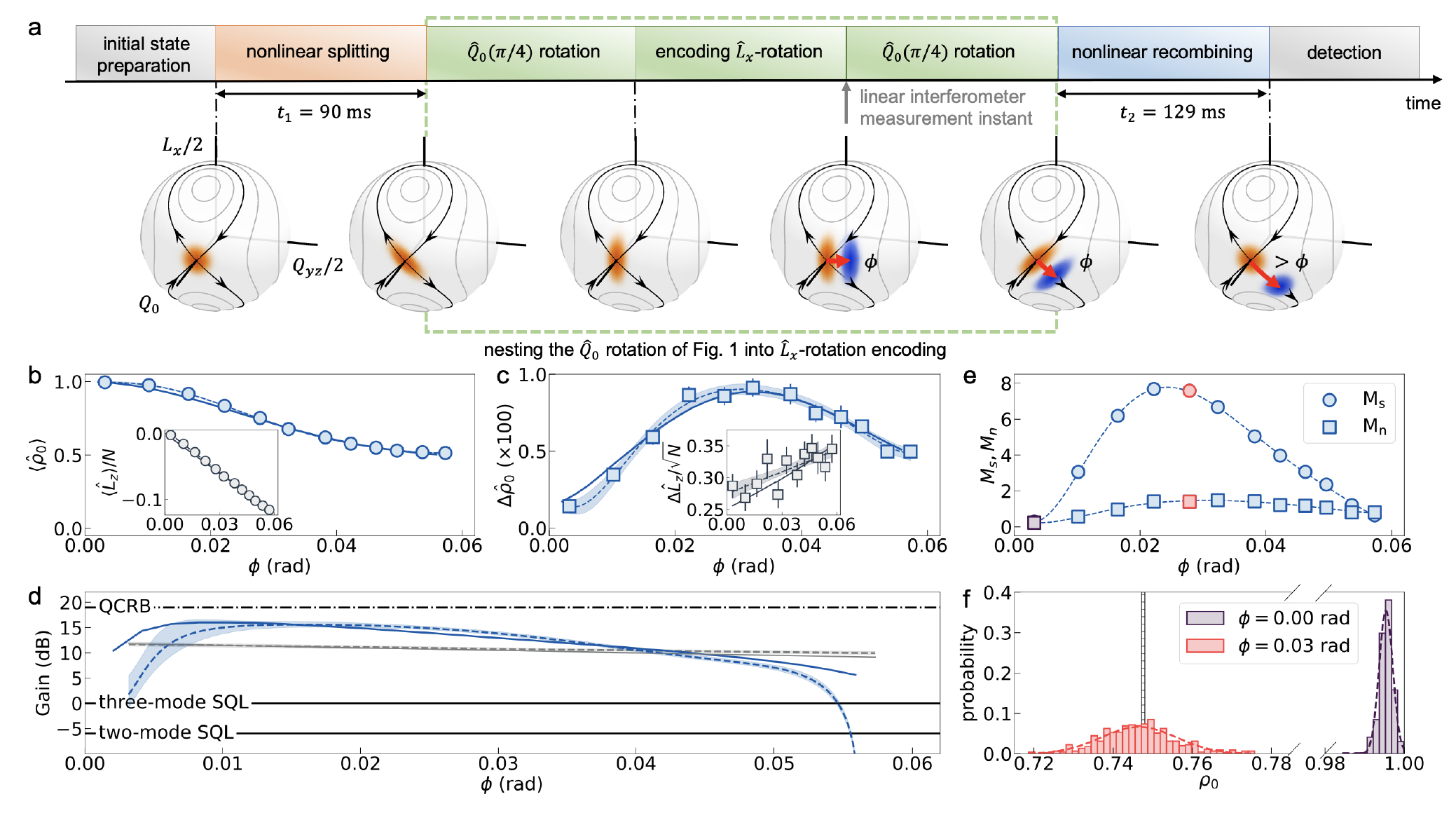

[5].  Tian-Wei Mao, Qi Liu, Xin-Wei Li, Jia-Hao Cao, Feng Chen, Wen-Xin Xu, Meng Khoon Tey, Yi-Xiao Huang and Li You, Nature Physics (2023): 19(11),1585-1590.

This work was recognized with a Nomination Award (Fundamental Research) in the 2023 China’s Top 10 Optical Breakthroughs.

Joint Estimation of a Two-Phase Spin Rotation beyond Classical Limit^[6]

Quantum metrology employs entanglement to enhance measurement precision. The focus and progress so far have primarily centered on estimating a single parameter. In diverse application scenarios, estimation of more than one single parameter is often required. Joint estimation of multiple parameters can benefit from additional advantages for further enhanced precision. Here we report quantum-enhanced estimation of simultaneous spin rotations around two orthogonal axes, making use of spin-nematic squeezing in an atomic Bose-Einstein condensate. Aided by the F = 2 atomic ground hyperfine manifold coupled to the nematic-squeezed F = 1 states as an auxiliary field through a sequence of microwave (MW) pulses, multiple spin-1 observables are simultaneously measured, reaching an enhancement factor 3.3 to 6.3 decibels (dB) beyond the classical limit over a wide range of rotation angles. Our work realizes the first quantum enhanced multiparameter estimation using entangled massive particles. The techniques developed and the protocols implemented also highlight the application of two-mode squeezed vacuum states in quantum-enhanced sensing of noncommuting spin rotations simultaneously.

Joint estimation of spin rotation angles around Lx and Ly. Figure(a): Schematics of the joint estimation interferometry protocol with quasiprobability distributions for the states plotted in the {Lx,Qyz} and {Ly,Qxz} planes, respectively. US, UR, and Uφ denote the unitary evolutions generated by spin-mixing, spinor phase rotation, and encoding spin rotation, respectively.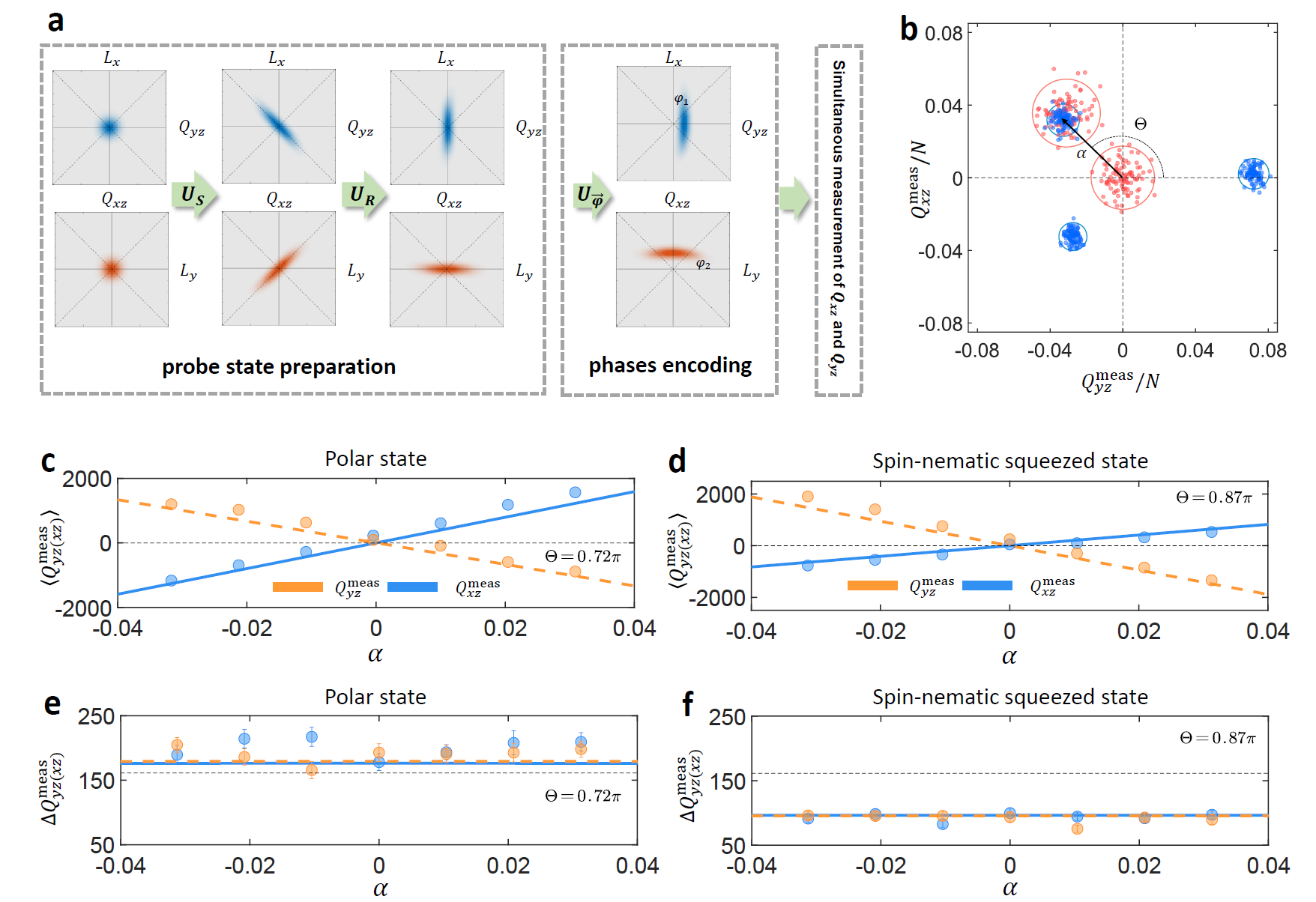

[6].  Jia-Hao Cao, Xinwei Li, Tianwei Mao, Wenxin Xu, and Li You, Physical Review Letters (2025): 135(2),023403.